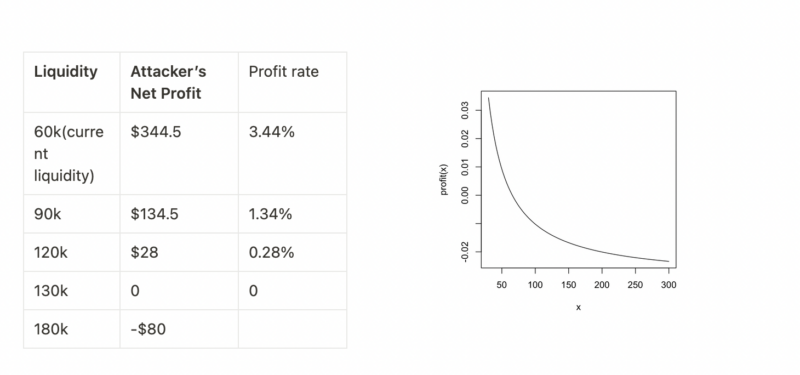
How Much Liquidity is Needed to Solve Sandwich Attacks?
Base Model
Here we assume there is a liquidity pool on Ethereum. Two assets GCR-USDC, with a relation xy=k, where x,y represent the quantity of asset GCR, USDC in the pool, and k is the product of their quantity, which is a constant given the property of the AMM mechanism. (We just ignore pool transaction fee since it is quite small and negligible in this question)
Sandwich Attacks is basically a front-running strategy to transact just before a large trade in a pool. For example, Alice trades GCR-USDC pair in Uniswap V2. She wants to buy ^x amount of GCR tokens with ^y USDC. After she approves her transaction with an input of ^y amount of USDC, her transaction is pending and waiting for a miner to package her transaction. Just right before her transaction is packaged, a front-running bot discovered her transaction and traded before her transaction is finalized. We assume the front-running bot puts ^y{a} USDC into the pool at this time(an “a” here means attack, to distinguish with Alice’s money), with a higher network transaction fee to front-run Alice. What happened then is the bot’s transaction is packaged before Alice’s, which means Alice trades at a higher price than she expected because here is a bot traded before her. We just use the following formulas to describe it in a formalized manner:
Go here to read the rest of the post and see the full formula.












